Inputs and Outputs
This week, your student will be working with functions. A function is a rule that produces a single output for a given input.
Not all rules are functions. For example, here’s a rule: the input is “first letter of the month” and the output is “the month.” If the input is J, what is the output? A function must give a single output, but in this case the output of this rule could be January, June, or July, so the rule is not a function.
Here is an example of a rule that is a function: input a number, square it, then multiply the result by

We could also represent this function with an equation,
Here is a task to try with your student:
Jada can buy peanuts for $0.20 per ounce and raisins for $0.25 per ounce. She has $12 to spend on peanuts and raisins to make trail mix for her hiking group.
- How much would 10 ounces of peanuts and 16 ounces of raisins cost? How much money would Jada have left?
- Using
p for pounds of peanuts andr for pounds of raisins, an equation relating how much of each they buy for a total of $12 is0.2p+0.25r=12 . If Jada wants 20 ounces of raisins, how many ounces of peanuts can she afford? - Jada knows she can rewrite the equation as
r=48−0.8p . In Jada’s equation, which is the independent variable? Which is the dependent variable?
Solution:
- 10 ounces of peanuts would cost $2 since
0.2⋅10=2 . 16 ounces of raisins would cost $4 since0.25⋅16=4 . Together, they would cost Jada $6, leaving her with $6. - 35 ounces of peanuts. If Jada wants 20 ounces of raisins, then
0.2p+0.25⋅20=12 must be true, which meansp=35 . p is the independent variable andr is the dependent variable for Jada’s equation.
Linear Functions and Rates of Change
This week, your student will be working with graphs of functions. The graph of a function is all the pairs (input, output), plotted in the coordinate plane. By convention, we always put the input first, which means the inputs are represented on the horizontal axis and the outputs on the vertical axis.
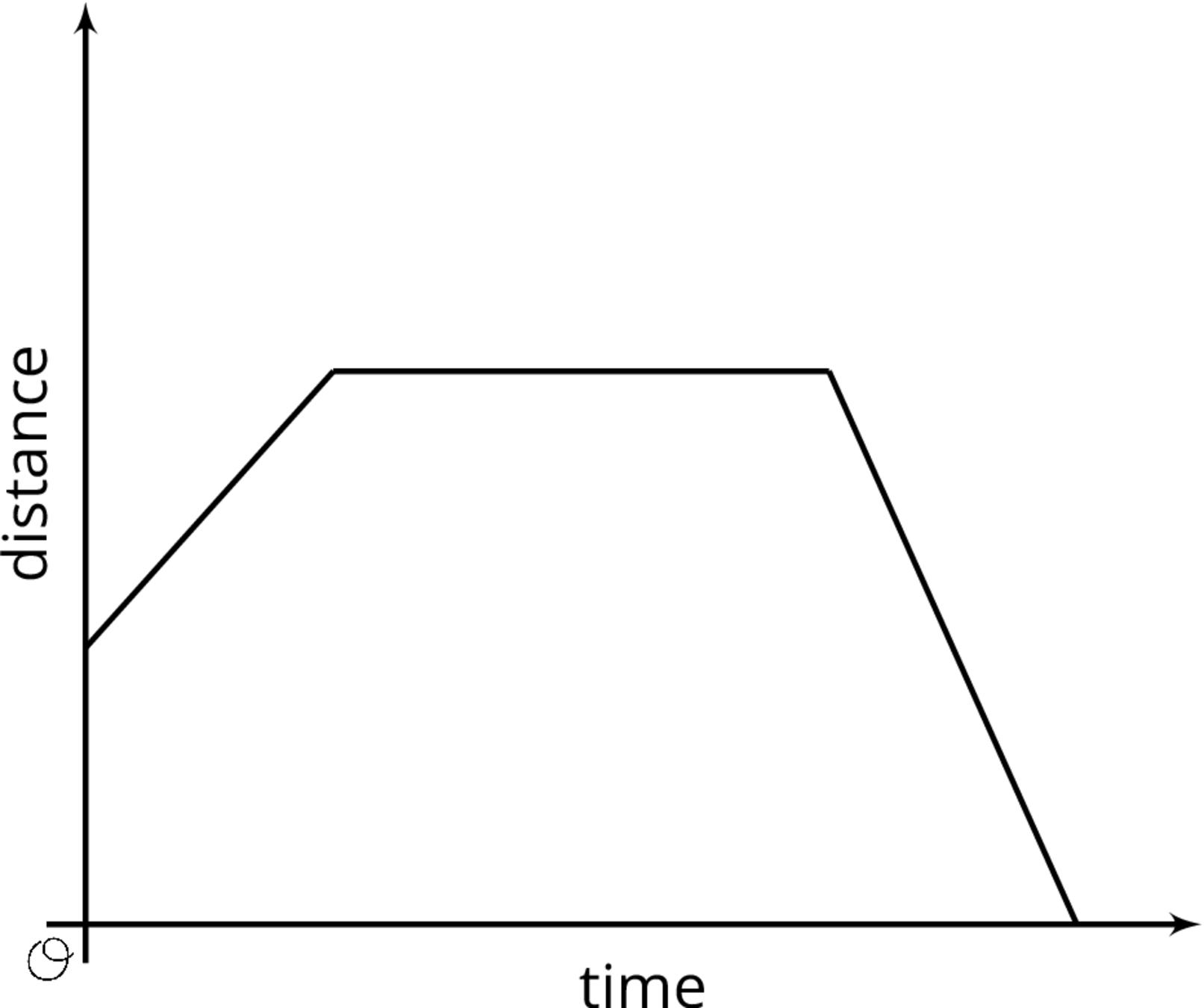
For a graph representing a context, it is important to specify the quantities represented on each axis. For example this graph shows Elena’s distance as a function of time. If it is distance from home, then Elena starts at some distance from home (maybe at her friend’s house), moves further away from her home (maybe to a park), stays there a while, and then returns home. If it is distance from school, the story is different.

The story also changes depending on the scale on the axes: is distance measured in miles and time in hours, or is distance measured in meters and time in seconds?
Here is a task to try with your student:
Match each of the following situations with a graph (you can use a graph multiple times). Define possible inputs and outputs, and label the axes.
- Noah pours the same amount of milk from a bottle every morning.
- A plant grows the same amount every week.
- The day started very warm but then it got colder.
- A cylindrical glass contains some partially melted ice. The more water you pour in, the higher the water level.

Solution:
- Graph B, input is time in days, output is amount of milk in the bottle
- Graph A, input is time in weeks, output is height of plant
- Graph C, input is time in hours, output is temperature
- Graph A, input is volume of water, output is height of water
In each case, the horizontal axis is labeled with the input, and the vertical axis is labeled with the output.
Cylinders and Cones
This week your student will be working with volumes of three-dimensional objects. We can determine the volume of a cylinder with radius
- The volume of a rectangular prism is a result of multiplying the area of its base by its height.
- The base of the cylinder is a circle with radius
r , so the base area isπr2 .
Just like a rectangular prism, the volume of a cylinder is the area of the base times the height. For example, let’s say we have a cylinder whose radius is 2 cm and whose height is 5 cm like the one shown here:

The base has an area of
Here is a task to try with your student:

This cylinder has a height and radius of 5 cm. Leave your answers in terms of
- What is the diameter of the base?
- What is the area of the base?
- What is the volume of the cylinder?
Solution:
- 10 cm. The diameter is
2⋅r , and2⋅5=10 . 25π cm2. The area isπ times the radius squared, or52⋅π .- 125
π cm3. The volume is the area of the base times the height. The area of the base here is 25π , so the volume is125π cm3 since25π⋅5=125π .
Dimensions and Spheres
This week, your student will compare the volumes of different objects. Many common objects, from water bottles to buildings to balloons, are similar in shape to rectangular prisms, cylinders, cones, and spheres—or even combinations of these shapes. We can use the volume formulas for these shapes to compare the volume of different types of objects.
For example, let’s say we want to know which has more volume: a cube-shaped box with an edge length of 3 centimeters or a sphere with a radius of 2 centimeters.
The volume of the cube is 27 cubic centimeters since
Here is a task to try with your student:
A globe fits tightly inside a cubic box. The box has an edge length of 8 cm.
- What is the volume of the box?
- Estimate the volume of the globe: is it more or less than the volume of the box? How can you tell?
- What is the diameter of the globe? The radius?
- The formula for the volume of a sphere (like a globe) is
V=43πr3 . What is the actual volume of the sphere? How close was your estimate in the previous problem?
Solution:
- 512 cm3. The box is a cube, so its volume is
83 cubic centimeters. - Answers vary. The number should be less than 512 cm3 since the volume of the globe must be less than the volume of the box. Possible explanation: it fits entirely inside the box, so it takes up less space. Since you can fit the globe inside the box and there is still space left over, the box has more volume.
- Since the globe fits tightly inside the cubic box, the diameter of the globe must be the same as the edge length of the box, 8 cm. This means the radius is 4 cm.
2563π or about 268 cm3. Since the side length of the cube is 8 cm, the radius of the globe is half of that, or 4 cm. The volume of the globe is therefore43π⋅43=2563π .
IM 6–8 Math was originally developed by Open Up Resources and authored by Illustrative Mathematics, and is copyright 2017-2019 by Open Up Resources. It is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). OUR's 6–8 Math Curriculum is available at https://openupresources.org/math-curriculum/.